집단 비교에 대한 개념을 체크하는 문제 풀이를 먼저 진행했다.
각 검정 방법이 어떤 상황에 사용하는지에 대해 익혔다.
그 후 상관 분석, 회귀 분석 등에 대해 학습했다.
제3의 변인, 상관과 인과, 심슨의 역설 관련 부분이 특히 흥미로웠다.
상관 분석
상관 계수(correlation coefficient)
- 두 변수의 연관성을 -1 ~ +1 범위의 수치로 나타낸 것
- 두 변수의 연관성을 파악하기 위해 사용
- 어휘력과 독해력의 관계
- 주가와 금 가격의 관계
- 엔진 성능과 고객만족도의 관계

상관계수의 해석
부호
- 플러스(+) : 두 변수가 같은 방향으로 변화(하나가 증가하면 다른 하나도 증가)
- 마이너스(-) : 두 변수가 반대 방향으로 변화(하나가 증가하면 다른 하나는 감소)
크기
- 0 : 두 변수가 독립, 한 변수의 변화로 다른 변수의 변화를 예측하지 못한다.
- 1 : 한 변수의 변화와 다른 변수의 변화가 정확히 일치
상관계수는 기울기와 다른 개념이므로 주의

상관계수와 비단조적 관계
- 상관계수는 우상향 또는 우하향하는 단조적 관계를 표현
- 복잡한 비단조적 관계는 잘 나타내지 못한다
- 상관계수가 낮다고 해서 관계가 없는 것은 아니다.

위 그림은 전부 다른 비단조적 관계를 가지지만 상관계수는 모두 0이다.
공분산
X의 편차와 Y의 편차를 곱한 것의 평균 (X=Y이면 분산과 같다)

우상향하는 추세인 경우 +방향으로 커진다.
우하향하는 추세인 경우 -방향으로 커진다.

공분산은 이론상 범위가 무한대인데, -1 ~ +1 범위로 만든 것이 피어슨 상관계수
피어슨 적률 상관계수
- 가장 대표적인 상관계수
- 다른 상관계수들도 있지만 상관계수라고 한다면 일반적으로 피어슨 적률 상관계수를 의미

- 선형적인 상관계수를 측정
- 공분산을 두 변수의 표준편차로 나누어 -1 ~ +1 범위로 만든 것
스피어만 상관계수
- 실제 변수값 대신 그 서열을 사용하여 피어슨 상관계수를 계산
- 한 변수의 서열이 높아지면 다른 변수의 서열도 높아지는지를 나타낸다.
- 두 변수의 관계가 비선형적이나 단조적일 때 사용
상관분석 가설검정 순서

상관계수의 크기 해석
- 상관계수의 크기에 대해서는 몇 가지 권장 기준이 있으나(예시: Cohen, 1988), 엄밀한 근거에 바탕을 둔 것은 아니다.
- 낮다 : ~0.1
- 중간 : 0.1 ~ 0.5
- 높다 : 0.5~
- 실제 의사결정에서는 상대적으로 비교하는 것이 바람직하다.
- 예를 들어 상관계수 0.2인 요소 A와 0.3인 요소 B가 있고, 예산상 한 가지 요소만 고려할 수 있다면 B를 고려한다.
상관과 인과(correlation and causation)
두 변수의 상관관계는 인과관계를 담보하지 않는다.
- 상관관계가 있다고 해서 반드시 인과관계가 있는 것은 아니다.
- 제3변인의 존재
- 이질적인 집단들의 합 (심슨의 역설)
- 극단치(outliers)
제3의 변인
- 예시 : 도시 내 범죄 발생 건수와 종교 시설의 수 사이에 양의 상관 관계가 있다.
- 범죄가 많아서 종교에 의존하는 것인가? 또는 종교가 범죄를 부추기는가?
- 사실은 인구가 많아지면 범죄도 늘고, 종교 시설도 많아지는 것이다.
=> 상관관계로 인과관계를 섣불리 예단하는 오류는 흔하다. 주의하자.

제3의 변인 예시 : 이혼율과 마가린 소비량의 관계
=> 매우 높은 상관관계가 있지만 우연의 일치일 뿐이다. 인과관계가 있지 않다.
심슨의 역설
- 각 집단별(부분) 상관관계와 전체 총합의 상관관계는 다를 수 있다.
- 상관분석 결과가 예상과 다를 경우, 이질적인 하위 집단들이 존재하는지 살펴봐야 할 수도 있다.
Python 상관 분석 실습
# 주행 거리와 중고차 가격의 scatter plot sns.scatterplot(x='mileage', y='price', data=df)
중고차 거래 데이터셋 df를 활용했다.

# 주행 거리와 가격의 상관계수 확인 pg.corr(df['mileage'], df['price'])
음의 상관 계수를 확인할 수 있다.

회귀 분석
지도학습(supervised learning)
- 독립변수 x를 이용하여 종속변수 y를 예측하는 것
- 독립변수(independent variable) : 예측의 바탕이 되는 정보, 인과관계에서 원인, 입력값
- 종속변수(dependent variable) : 예측의 대상, 인과관계에서 결과, 출력값
통계에서 예측(prediction)의 의미
- 통계학에서 예측은 어떤 값에 대한 추론을 의미한다.
- 시간적인 의미가 아니다.
- 지도학습에서 예측은 변수들 사이의 패턴을 파악하여 한 변수로 다른 변수를 추론하는 것
- 시계열 분석 등에서 하는 미래에 대한 예측은 forecasting이라고 구분한다
종속변수에 따른 지도학습의 구분
회귀분석(regression)
- 종속변수가 연속
- (예측값 – 실제값)으로 정확성을 계산
분류분석(classification)
- 종속변수가 범주형
- 예측의 정확성을 다른 방식으로 계산
선형 모형
ŷ = wx + b
ŷ : y의 예측치
x : 독립변수
w : 가중치 또는 기울기
b : 절편(x=0일 때, y의 예측치)
회귀분석 예시 : 위도에 따른 피부암으로 인한 사망
- 독립변수(x) : 위도
- 종속변수(y) : 천만명당 사망자 수

잔차(residual)
실제값과 예측값의 차이
잔차분산 : 잔차를 제곱하여 평균낸 것
분산 : 편차(실제값과 평균의 차이) 제곱의 평균
=> 예측을 평균으로 하면 잔차분산과 분산이 같다
잔차분산이 크다 : 예측이 잘 맞지 않다
잔차분산이 작다 : 예측이 잘 맞는다
최소제곱법(Ordinary Least Squares)
잔차 분산이 최소가 되게 하는 w, b 등 계수를 추정하는 방법
최소'제곱'법인 이유 : 분산의 계산에 제곱이 들어가기 때문
가장 널리 사용되는 추정 방법
Python을 이용한 회귀분석
from statsmodels.formula.api import ols중고차 주행거리(독립변수)에 따른 가격(종속변수)
# 종속변수(y) ~ 독립변수(x) 형식 m = ols("price ~ mileage", data = df).fit() m.summary()
절편과 기울기를 확인해보자.
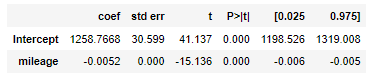
Intercept(절편) 1258.7668 : 주행거리 0km일 때
mileage(기울기) -0.0052 : 1만km마다 52만원꼴로 가격이 떨어진다
sns.regplot(data=df,x='mileage', y='price')regplot 확인
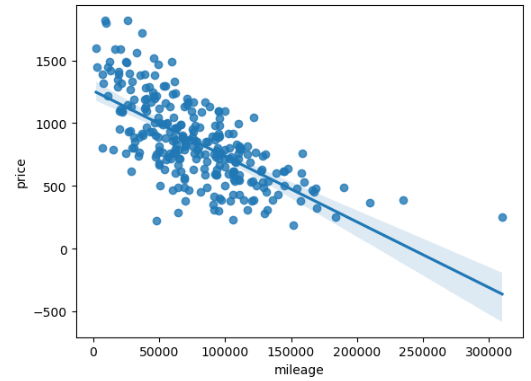
즉, 회귀식은 price = 1258.7668 - 0.0052 * mileage이다.
regplot에서 선으로 표현된다.
R 제곱(R Squared)
회귀 분석에서 예측의 정확성을 알기 쉽게 판단할 수 있게 만든 지표 (0~1)
R² = 1 - 잔차분산 / 분산
- R제곱 = 0 : 분석결과가 y의 예측에 도움이 안 된다.
- R제곱 = 1 : y를 완벽하게 정확히 예측할 수 있다.
R 제곱 읽는 법
- R제곱 읽을 때는 "모형이 종속변수 분산의 ~%를 설명한다"라고 한다.
- 예시 : R제곱 = 0.3 => "분산의 30%를 설명한다"
- 중고차 주행 거리가 가격 분산의 45.7%를 설명한다
- R제곱은 TSS(분산)에 비해 RSS가 얼마나 작아졌는지를 나타낸다.
- TSS와 RSS는 모두 평균, 또는 예측에 대한 변산성(불확실성)
- 변산성이 줄어들었다 => 불확실성이 줄어들었다 => 설명이 되었다
다중회귀분석
다중회귀분석
독립변수가 2개 이상인 회귀분석
- Python에서는 관계식에서 +로 변수를 구분
- 종속변수 ~ 독립변수 + 독립변수 + ...
- price ~ mileage + model
- 더하라는 뜻이 아님에 주의
통계적 통제
- 독립변수 x와 상관관계가 높은 요소 z가 존재할 경우
- z가 종속변수 y에 미치는 영향이 x의 기울기에 간접 반영될 수 있다.
- 실험적 통제 : 데이터에서 z를 일정하게 유지하여, z의 영향을 제거
- 통계적 통제 : z를 모형에 독립변수로 함께 포함하여, x의 기울기에 z의 영향이 간접 반영되지 않도록한다.
=> 예시 : 주행거리에 따른 중고차 가격은 사실 주행거리와 연식에 상관관계가 높으므로 연식이 간접 반영된 것으로 볼 수 있다.
=> 실험적 통제는 연식은 고정시킨 상태로 주행거리만 다르게하여 비교
- 실험적 통제는 현실적으로 어려운 경우가 많다
=> 통계적 통제는 독립변수로 주행거리와 연식을 함께 포함
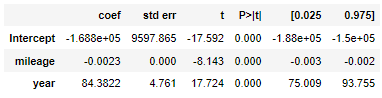
m = ols('price ~ mileage + year', df).fit() m.summary()
주행 거리와 연식이 가격에 미치는 영향 => 표준화가 필요
표준화(Standardization)
다중회귀분석에서 독립변수끼리 단위가 다르므로 종속변수에 대한 영향력을 비교하기 어렵다
- 예시 : 연식은 1년 단위, 주행거리는 1km단위이므로 비교가 어렵다
표준화 식 :

- 표준화를 하면 평균 = 0, 표준편차 = 1이 된다
- 표준화를 통해 변수의 단위를 제거하여 상대적인 영향력을 비교할 수 있다.
- 예측이 더 정확해지는 것은 아니다.
- scale 함수를 통해 표준화가 가능하다.
m = ols('price ~ scale(mileage) + scale(year)', df).fit() m.summary()
scale 함수 사용 후 비교
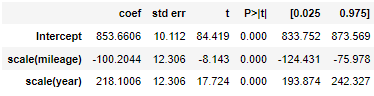
mileage는 1표준편차만큼 오르면 가격이 -100.2만원 떨어진다.
year는 1표준편차만큼 오르면 가격이 218.1만원 오른다.
=> 거리, 연 단위를 없앰으로써 year가 더 영향이 크다는 것을 알 수 있다.
Python 다중회귀분석 예시
df_iqsize = pd.read_excel('iqsize.xlsx') df_iqsize.head()
PIQ : 동작성 지능
Brain : 두뇌의 크기(부피)
Height : 키
Weight : 체중
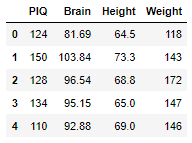
모형 : 동작성 지능을 종속 변수로, 몸무게와 키, 두뇌 크기를 독립변수로 다중회귀분석
m = ols('PIQ ~ Height + Weight + Brain', df_iqsize).fit() m.summary()
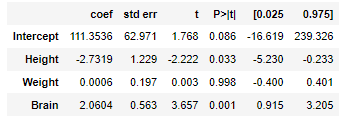
다른 변수가 같다는 조건, 유의수준 5%에서 동작성 지능이
키가 커질수록 : 감소한다
몸무게가 무거워질수록 : 결론을 유보
두뇌가 커질수록 : 증가한다
'AI SCHOOL > TIL' 카테고리의 다른 글
| [DAY 39] 미드프로젝트1 시작, 카페 체인별 매장 정보 수집과 전처리 (0) | 2023.02.20 |
|---|---|
| [DAY 38] 통계 마지막 날 - 모형 선택, overfitting, 교차 검증, 단계적 회귀분석, 다중공선성, 잔차분석, 상호작용 (0) | 2023.02.17 |
| [DAY 36] 효과 크기, 대응표본 t-검정, 분산 분석, 카이제곱 검정, 맥니마 검정 (0) | 2023.02.15 |
| [DAY 35] 표집(sampling), 추정, 통계적 가설 검정, A/B 테스트 (0) | 2023.02.14 |
| [DAY 34] 통계 강의 시작 - 변수, 확률분포, 확률질량함수, 중심극한정리, 기술통계, 상자수염그림, 모집단과 표본 (0) | 2023.02.13 |




댓글