Special Lecture인 통계분석이 1주일동안 진행될 예정이다.
강의를 집중해서 듣고 데이터분석을 위한 통계 역량을 키워야겠다.
통계를 배우는 이유(활용 예시)에 대한 소개를 시작으로 강의가 진행되었다.
통계로 무엇을 할 수 있는가
전문가 판단 vs 통계적 예측
미네소타대학교 심리학 교수 폴 밀, 1954
"학업성, 정신질환의 예후 등에서 전문가의 판단보다 통계적 예측이 더 정확하다."
이러한 밀의 연구 이후 수십년간 논란이 되었고 136개의 연구를 검토한 결과 통계적 예측이 더 정확했다.
- 통계 우위(63개), 동률(65개), 전문가 우위(8개)
전문가의 판단은 내외부적 잡음에 영향을 받는 반면 통계적 모델을 통한 예측은 잡음에 영향을 받지 않는다.
통계적 예측이 충분히 사용되지 않는 이유
전문가보다 정확한 통계가 왜 충분히 사용되지 않을까?
1. 타당성의 환상 : 스스로 생각하는 판단의 정확성과 실제 정확성 사이의 괴리
2. 판단을 직접 내릴 때 얻는 만족감(퍼즐이 맞춰지는 느낌)이 보상으로 작용
3. 통계적 지식의 부족과 반감
4. 통계가 완벽하기를 기대하며 오류에 지나치게 실망
- 인간의 실수에는 관대하다
- 예시 : 자율주행 자동차가 사람만큼 사고를 낸다면? => '역시 AI는 아직 일러' 라고 생각한다.
5. 예측에서 단순성과 복잡성에 대한 오해
대상의 특성을 수치로 표현
- 관찰할 수 있는 특성은 무엇이든 수치로 표현할 수 있다.
- 양적인 것은 물론, 질적인 특성도 수치화 가능
- 만족도 등 수치가 객관적이지 않아도 된다.
- 수치가 대상을 파악하기에 좋은 성질을 가지고 있는가?
- 수치들을 잘 요약하여 효과적으로 정보를 전달
부분을 통해 전체를 추측
- 대부분의 경우 우리는 대상의 일부만을 관찰할 수 있다.
- 여론조사 : 전국민에게 전부 조사할 수 없으므로 소수를 대상으로 조사
- 면접 : 한 개인의 인생에서 한 순간만을 조사
- 현실에서는 우연과 불확실성이 존재한다.
- 성실한 사람도 면접에 늦을 수 있다.
비교하기
- 여러 대상을 비교
- 임상시험
- A/B 테스트
- 대상들 사이에 어떤 차이가 있으며 대상 자체의 특성에 기인한 것인가?
예측하기
- 어떤 특성은 다른 특성보다 쉽게 알 수 있다.
- 주택의 입지, 교통, 환경 등은 쉽게 파악 가능
- 가격은 거래가 성사되어야 파악 가능
- 한 대상의 여러 특성들은 서로 관련이 있다.
- 쉽게 알 수 있는 특성들로부터 알기 어려운 어떤 특성을 예측할 수 있다.
- 예측은 미래에 대한 예측만을 의미하는 것은 아니다.
영향력을 미치는 변수 찾기
- 대상의 한 가지 특성은 여러 특성으로부터 영향을 받는다
- 고객 만족도 : 가격, 응대, 서비스의 질, 경쟁 서비스의 특성 등에 영향을 받는다.
- 어떤 특성은 다른 특성보다 직접적으로 변화시키기 쉽다.
- 고객 만족도를 직접 높일 수는 없지만, 더 친절하게 응대하도록 변화하는 것은 쉽다.
- 목적으로 하는 특성에 영향이 큰 변수를 분별
- 해당 변수를 높이거나 낮추어 목적으로 하는 특성을 조절
지수 만들기
- 대상의 특성 중에는 직접적으로 관찰하기 어려운 것이 있다.
- 고객 만족도, 사랑, 유전자 등
- 이러한 특성은 관찰 가능한 다른 특성들과 연관을 가진다.
- 고객 만족도가 높다면? 재구매, 추천 등의 행동을 많이 하게 된다.
- 관찰 가능한 특성들을 바탕으로 관찰하기 어려운 특성들을 지표화할 수 있다.
- 이들의 지표를 통해 관찰하기 어려운 대상을 통계적으로 다룰 수 있다.
- 대상 자체가 실재하지 않는다 해도, 이 지표를 통해 의사결정이 쉬워진다.
비슷한 것끼리 모으기
- 비슷한 것을 모아서 하나의 집단으로 인식하면 편리한 경우가 있다.
- 비슷한 고객들에게 같은 프로모션이나 추천
- 합정-홍대는 같은 상권, 신촌은 별개의 상권
- 대상의 다양한 특성들을 바탕으로 비슷한 것끼리 모을 수 있다.
통계는 어렵다
통계는 왜 어려운가?
- 통계학은 매우 늦게 형성된 학문이다.
- 인류는 학문을 4000년가량 했지만 통계학은 19세기 후반~20세기 초반에 시작되었다.
- 대학에 통계학과가 설립된 것은 1911년 영국 UCL이 처음
- 기존 인류의 자연스러운 사고방식과는 동떨어져 있다.
- 통계학은 특성상 많은 계산이 필요 -> 초기 통계학이 형성된 20세기 초반에는 현대 컴퓨터가 없다 -> 이해하기 쉬운 논리보다 손으로 쉽게 계산할 수 있는 형태의 특정한 방법론들이 발전
- 통계학의 개념들은 일상적, 직관적 관점에서는 이해가 어렵다
- 해결책? 직관적 관점에서 이해하지 말고, 통계적 관점을 수용할 필요
이상한 통계학 용어
통계학의 어려움을 가중시키는 점 중 하나는 이상한 용어다.
- 번역이 이상한 경우 : 모수
- 어머니와 관련이 없고 분모와도 관련이 없다.
- 역사적 과정을 거쳐 의미가 변한 경우 : 회귀분석
- 돌아가는 것과는 직접적 관련이 없다.
- 만든 사람들의 사고 방식이 조금 이상(?)한 경우 : 통계적 가설 검정
- 일반적 과학에서의 가설 검정과는 전혀 다른 철학적 관점
=> 용어를 보고 뜻을 대충 짐작하면 안 된다.
변수의 종류
범주형 변수(categorical variable)
- 종류, 이름 등이 해당
- 숫자로 표시하더라도 양적인 개념이 아니다.
- 덧셈 등 대부분 연산이 의미가 없다.
- 순서가 있을 수도 있으나 간격이 일정하지 않다.
- 예시 : 주거 형태, 학력, 고향, 출석 등
연속형 변수(continuous variable)
- 연속적인 형태
- 간격이 일정하며 덧셈, 뺄셈 등의 연산이 의미가 있다.
- 예시 : 무게, 나이, 거리, 시간, 시험 점수 등
=> 만족도는 엄격히 따지면 범주형이지만 실무적으로는 연속형으로 취급하는 경우도 많다.
타당도(validity)와 신뢰도(reliability)
타당도 : 측정하고자 하는 것을 잘 측정하는 정도
신뢰도 : 측정 결과가 일정한 정도

기본적으로 타당도가 높아야하고 신뢰도는 두 번째 문제이다.
그러나 타당도를 정확히 알기 어려운 경우가 많다. 그런 경우 신뢰도라도 높아야한다.
타당도를 알 수는 있지만 너무 큰 비용이 드는 경우 타당도를 어느정도 양보해야한다.
확률 분포(probability distribution)
확률 분포 : 확률 변수가 특정한 값을 가질 확률을 나타내는 함수
- 이산(discrete) 확률분포 : 가질 수 있는 값이 정수
- 연속(continuous) 확률분포 : 가질 수 있는 값이 실수
세상에는 수많은 확률 분포가 존재하며 분석을 쉽게 하기 위해서 수학적으로 단순화, 추상화된 확률 분포들을 많이 사용한다.
베르누이 분포(Bernoulli distribution)
동전 던지기와 같이 둘 중에 한 가지 결과만 나올 수 있는 경우
- 둘 중에 한 가지 결과가 나오는 현상에 모두 적용 가능
- 고객의 이탈/유지
- 기계의 작동/고장
- 시험 합격/불합격
이항 분포(binomial distribution)
0과 1만 나오는 시행을 n번 했을 때 합계의 분포
베르누이 분포는 n=1인 경우의 이항 분포
이항 분포 시뮬레이션
구매율이 30%인 100명의 고객이 매장을 방문할 때, 몇 명의 고객이 구매를 하는가? * 365회 반복
import matplotlib.pyplot as plt
from scipy.stats import binom
data = binom.rvs(n=100, p=0.3, size=365)
plt.hist(data, bins=40, range=[10, 50], edgecolor='black')
plt.show()

이항분포의 확률질량함수와 누적분포
확률질량함수(probability mass function)
- 구매율30%인 고객이 100명 방문했을 때 딱 30명이 구매할 확률
binom.pmf(k=30, n=100, p=0.3)
# 실행 결과
0.08678386475342813
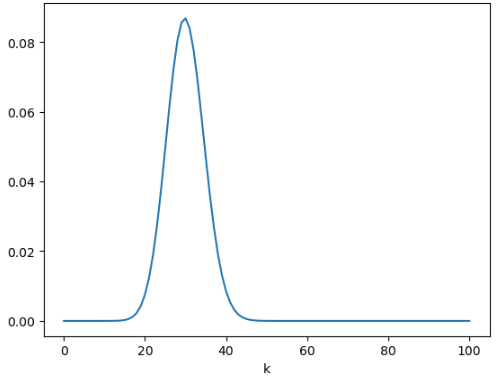
구매율이 0.3인 100명의 고객 중 k명이 구매할 확률 그래프
import numpy as np
x = np.arange(0, 101)
p = binom.pmf(k=x, n=100, p=0.3)
plt.plot(x, p)
plt.xlabel('k')
plt.show()
누적분포함수(cumulative distribution function)
딱 30명이 아닌, 0명~30명이 구매할 확률의 합
binom.cdf(k=30, n=100, p=0.3)
# 실행 결과
0.5491236007687914
구매율이 0.3인 100명의 고객 중 k명 이하가 구매할 확률 그래프
p = binom.cdf(k=x, n=100, p=0.3) # 누적
plt.plot(x, p)
plt.xlabel('k')
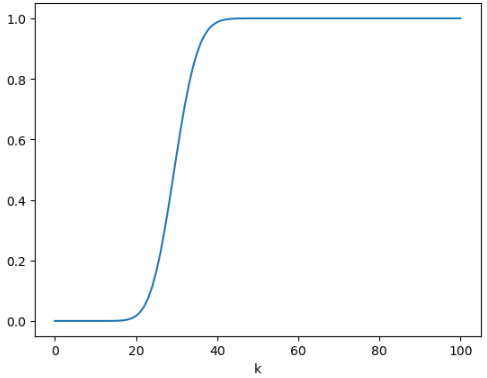
k=30에서 0.5 이상, k=40에서 거의 1에 가까운 값을 볼 수 있다.
정규 분포(normal distribution)와 중심극한정리(central limit theorem)
정규 분포(normal distribution)
연속확률분포
μ(뮤)와 σ2(시그마)에 따라 모양이 달라진다.
- μ(뮤)의 확률이 가장 높고 멀어질 수록 확률이 낮아진다.
- μ(뮤)를 기준으로 좌우 대칭
- σ2이 클수록 넓게 퍼진다.
- 가우시안 분포라고도 한다.
중심극한정리(central limit theorem)
어떤 확률분포에서 값을 n개 독립적으로 뽑아서 더하여 합계 s를 구할 경우 n이 커질 수록, s의 분포는 정규분포와 점점 비슷해진다.
예시 : 주사위는 1~6이 고르게 나오지만, 주사위를 10번 던져서 합계를 구하면 35 근처 값이 가장 많이 나온다.
이항분포의 경우
- 이항분포는 베르누이 분포에서 값을 n개 뽑아 더한 것과 같다.
- n이 커지면 정규분포와 비슷해진다.
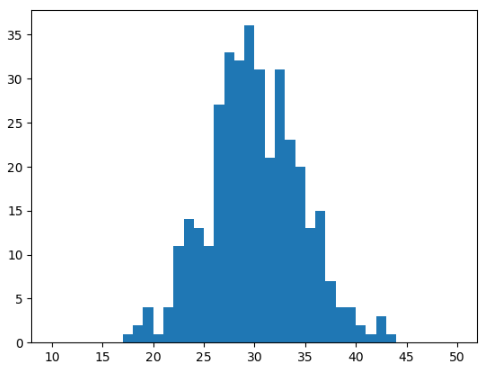
이항분포를 정규분포로 근사하여 시뮬레이션
from scipy.stats import norm
m = 30 # 100 * 0.3
s = np.sqrt(21) # np.sqrt(100*0.3*0.7)
data = norm.rvs(loc=m, scale=s, size=365) # loc은 평균 scale은 표준편차
plt.hist(data, bins=40, range=[10, 50])
plt.show()
norm.cdf(x=30, loc=m, scale=s)
# 실행 결과
0.5위의 정규분포를 통한 값과 아래 이항분포를 정규분포로 근사한 값과 비교해보자.
print(binom.cdf(k=30, n=100, p=0.3)) # 100회 시행
print(binom.cdf(k=300, n=1000, p=0.3)) # 1000회 시행
print(binom.cdf(k=3000, n=10000, p=0.3)) # 10000회 시행
# 실행 결과
0.5491236007687914
0.515593519814106
0.5049329838192946n이 커질수록 정규분포에 가까워짐을 알 수 있다.
기술 통계
기술 통계(descriptive statistics) : 데이터를 묘사, 설명
추론 통계(inferential statistics) : 데이터를 바탕으로 추론, 예측
중심 경향치: 데이터가 어디에 몰려있는가?
- 평균, 중앙값
분위수: 데이터에서 각각의 순위가 어느정도인가?
변산성 측정치: 데이터가 어떻게 퍼져있는가?
- 범위, IQR
- 분산, 표준편차
평균(mean) : n개의 값이 있을 때 그 합계를 n으로 나눈 것
- 평균은 극단값에 따른 영향을 크게 받는다.
- 10, 20, 30, 40, 50의 평균은 30
- 10, 20, 30, 40, 500의 평균은 120
예시: 1986년 미국 노스캐롤라이나 대학 (UNC) 졸업생 평균 초봉 조사
- 가장 높은 학과는 지리학과 (25만 달러)
- 당시 미국 대졸 평균 초봉은 2만 2천달러 수준
- 당시 마이클 조던이 UNC 지리학과를 졸업했기 때문에 지리학과 평균 초봉이 매우 올라간 것
중앙값(median): 값들을 크기 순으로 정렬했을 때 중간에 위치한 값
- 중앙값은 극단값에 따라 영향을 크게 받지 않는다.
- 10, 20, 30, 40, 50의 중앙값은 30
- 10, 20, 30, 40, 500의 중앙값은 30
- 중위수라는 표현도 많이 사용 (중위소득, 중위가격 등)
- 값이 짝수개 있을 경우는 가운데 두 값의 평균
- 10, 20, 30, 40의 중앙값은 20, 30의 평균 => 25
분위수(quantile): 크기순으로 정렬된 데이터를 q개로 나누는 위치의 값
- 대표적으로 사분위수, 백분위수가 있음
사분위수(quartile)
- 데이터를 4등분하는 위치
- 제1사분위수 → 1/4 지점
- 제2사분위수 → 2/4 지점 => median과 같다
- 제3사분위수 → 3/4 지점
- 영어 철자에 주의. 분위수(quantile), 사분위수(quartile)는 다르다
백분위수(percentile)
- 데이터에서 순위를 퍼센트로 표현
- 최솟값 = 0퍼센타일
- 제1사분위수 = 25퍼센타일
- 제2사분위수 = 50퍼센타일 => median과 같다
- 제3사분위수 = 75퍼센타일
- 상위 10% 값 = 90퍼센타일
- 최댓값 = 100퍼센타일
범위(range) : 최댓값 - 최솟값
df['price'].min(), df['price'].max() # 일상적 의미에서 범위
# (190, 1820)
df['price'].max() - df['price'].min() # 통계적 의미에서 범위
# 1630
사분위간 범위 InterQuartile Range (IQR)
제3사분위수 - 제1사분위수
- 극단값은 최솟값 또는 최댓값 근처에 있으므로 극단값의 영향이 적다.
# python을 이용한 IQR 계산
df['price'].quantile(0.75) - df['price'].quantile(0.25)
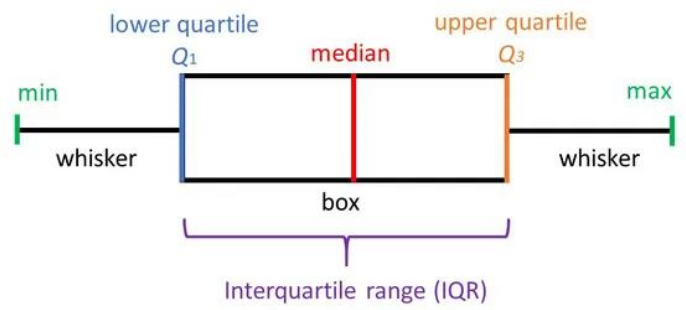
상자 수염 그림 box-whisker plot
- 제1사분위수 ~ 제3사분위수를 상자로 표현
- 중앙값은 상자의 가운데 굵은 선으로 표시
- 최솟값과 최댓값은 수염(whisker)으로 표시
- 수염의 최대 길이는 IQR의 1.5배까지, 수염을 넘어가는 경우는 점으로 표시한다.
편차, 분산, 표준편차
편차(deviation) : 값-평균
분산(variance) : 편차 제곱의 평균, 표준편차의 제곱
표준편차(standard deviation) : 분산의 제곱근
예시 : 원 데이터가 30, 40, 50인 경우
- 평균 : 40
- 편차 : -10, 0, +10
- 분산 : (100+100) / 3
- 표준편차 : √(100+100) / 3
커널 밀도 추정(kernel density estimation)
데이터의 밀도를 추정하여 그린 곡선
sns.histplot(x='price', data=df, bins=30, kde=True) # kde=True 사용
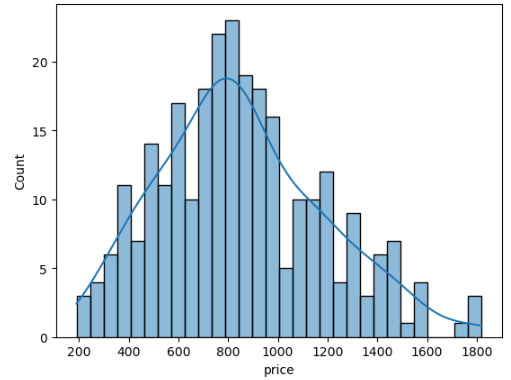
모집단과 표본
모집단(population) : 연구의 관심이 되는 집단 전체
표본(sample) : 특정 연구에서 선택된 모집단의 부분 집합
표집(sampling) : 모집단에서 표본을 추출하는 절차. 표본추출이라고도 한다
=> 대부분의 경우 집단 전체를 전수조사하기는 어려우므로 무작위 표본을 추출하여 모집단에 대해 추론
모수 population parameter
파라미터 parameter: 어떤 시스템의 특성을 나타내는 값
모수: 모집단 population의 파라미터 → 모집단의 특성을 나타내는 값
- 모집단의 평균: 모평균
- 모집단의 분산: 모분산
- 모수를 구하기 위해서는 전수조사가 필요 (사실상 어렵다)
- 주의! "표본의 크기"를 "모수"라고 하는 경우도 있으나 잘못된 표현
통계량 sample statistic
표본에서 얻어진 수로 계산한 값 (=통계치)
- 표본의 평균 (표본평균)
- 표본의 분산 (표본분산)
- 주의: "모집단의 통계량"이라는 표현은 없음 (통계량은 표본에서 구한 값)
- "표본의 모수" 같은 말도 없다 (모수는 모집단에서 구한 값)
- 추론 통계 inferential statistics: 표본 통계량을 일반화하여 모집단에 대해 추론 하는 것
'AI SCHOOL > TIL' 카테고리의 다른 글
| [DAY 36] 효과 크기, 대응표본 t-검정, 분산 분석, 카이제곱 검정, 맥니마 검정 (0) | 2023.02.15 |
|---|---|
| [DAY 35] 표집(sampling), 추정, 통계적 가설 검정, A/B 테스트 (0) | 2023.02.14 |
| [DAY 33] SQL 마지막 날 - 추천도서, 내용 정리, 연습문제 (0) | 2023.02.12 |
| [DAY 32] Week 8 Insight Day 미드프로젝트1 공지, 나 사용법 (0) | 2023.02.09 |
| [DAY 31] 버거지수, 상관계수, plotly와 folium을 이용한 지도 시각화 (1) | 2023.02.09 |



댓글